Conversion rate analysis

Let’s simulate user visits with 4 different browser versions, 1 bad and 3 good. Main languages of users are de/fr/en and they don’t make a significant difference on conversion. The version does and we want to detect it using Pairwise Wilcoxon Rank Sum Test to identify pairs with different conversion rate and Chi-squared Test to identify significant variables (it’s version, not language).

library(ggplot2)
generateVisitors=function(version, lang,cnt, success_rte) {
  data.frame(version=version, lang=lang,success=rbinom(cnt,1,rep(success_rte,cnt)))
}
generateVisitorData=function(bad_version_visitors, total) {
  df=data.frame()
  df=rbind(df, generateVisitors("good-version.1", "de",round(total*0.45),0.12))
  df=rbind(df, generateVisitors("bad-version.2", "en",bad_version_visitors,0))
  df=rbind(df, generateVisitors("good-version.3", "en",round(total*0.34),0.15))
  df=rbind(df, generateVisitors("good-version.4", "fr",round(total*0.11),0.12))
  df
}
df=generateVisitorData(70,870)
df[sample(1:nrow(df), size = 20),]

##            version lang success
## 17  good-version.1   de       0
## 508 good-version.3   en       0
## 657 good-version.3   en       0
## 357 good-version.1   de       0
## 529 good-version.3   en       0
## 744 good-version.3   en       1
## 633 good-version.3   en       0
## 439  bad-version.2   en       0
## 420  bad-version.2   en       0
## 32  good-version.1   de       0
## 455  bad-version.2   en       0
## 246 good-version.1   de       0
## 198 good-version.1   de       0
## 384 good-version.1   de       0
## 823 good-version.4   fr       0
## 403  bad-version.2   en       0
## 239 good-version.1   de       0
## 451  bad-version.2   en       0
## 335 good-version.1   de       1
## 178 good-version.1   de       0

aggregate(success ~ lang, df, mean)

##   lang   success
## 1   de 0.1352041
## 2   en 0.1338798
## 3   fr 0.1458333

aggregate(success ~ version, df, mean)

##          version   success
## 1 good-version.1 0.1352041
## 2  bad-version.2 0.0000000
## 3 good-version.3 0.1655405
## 4 good-version.4 0.1458333

pairwise.wilcox.test(df$success, df$version)

## 
##  Pairwise comparisons using Wilcoxon rank sum test 
## 
## data:  df$success and df$version 
## 
##                good-version.1 bad-version.2 good-version.3
## bad-version.2  0.0044         -             -             
## good-version.3 0.8042         0.0016        -             
## good-version.4 1.0000         0.0044        1.0000        
## 
## P value adjustment method: holm

pairwise.wilcox.test(df$success, df$lang)

## 
##  Pairwise comparisons using Wilcoxon rank sum test 
## 
## data:  df$success and df$lang 
## 
##    de en
## en 1  - 
## fr 1  1 
## 
## P value adjustment method: holm

chisq.test(table(df$version,df$success))

## 
##  Pearson's Chi-squared test
## 
## data:  table(df$version, df$success)
## X-squared = 13.312, df = 3, p-value = 0.004009

chisq.test(table(df$lang,df$success))

## 
##  Pearson's Chi-squared test
## 
## data:  table(df$lang, df$success)
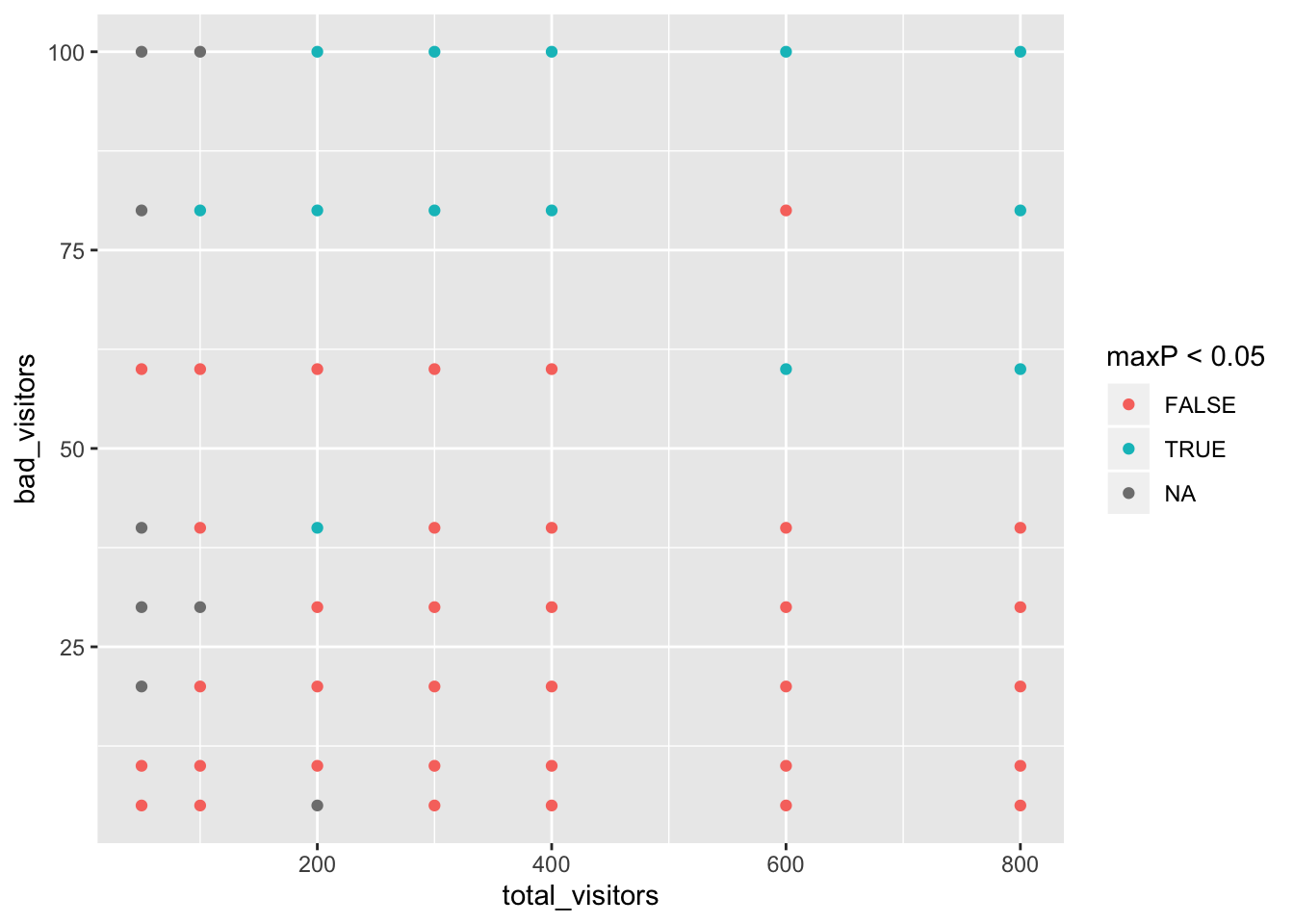
## X-squared = 0.095007, df = 2, p-value = 0.9536

Now let’s see how many visitors in total and with a bad version we need to detect problems with max p-value of 0.05 across pairs badVersion and goodVersion1,3,4.

ret=data.frame()
for (bad_visitors in c(5,10,20,30,40,60,80,100)) {
  for (total_visitors in c(50,100,200,300,400,600,800)) {
    df=generateVisitorData(bad_visitors, total_visitors)
    p=pairwise.wilcox.test(df$success, df$version)
    ret=rbind(ret, data.frame(bad_visitors=bad_visitors, total_visitors=total_visitors, maxP=max(c(p$p.value[1,1], p$p.value[2:3,2]))))
  }
}

ggplot(ret, aes(x=total_visitors, y=bad_visitors, colour=maxP<0.05))+geom_point()